Diseñar un Modelo Cripto Exitoso como Bitcoin.
Modelo deflacionario de emisión de tokens
En el artículo 1, estudiamos el modelo inflacionario, con una función donde la cantidad del token es la variable independiente y se emite el token, aunque el precio este a la baja, lo que lleva el proyecto al fracaso.
En este segundo artículo, estudiamos el modelo deflacionario: El precio es la variable independiente, reducir la emisión del token en el transcurso del tiempo, haciendo que el token sea un bien escaso.
El Bitcoin
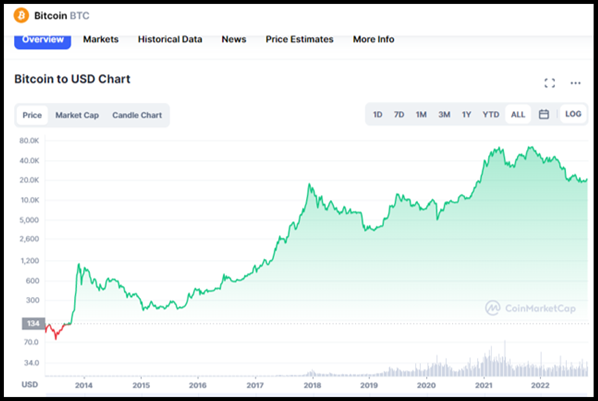
Aunque presenta volatilidad en el precio en el corto plazo, el Bitcoin ha tenido un comportamiento creciente en el largo plazo (grafico en escala logarítmica):
Algoritmo de función exponencial para describir la oferta de un producto (token)
I = Ingreso o capital obtenido medido en miles de Ether.
X = Cantidad de token en el mercado medido en millones.
Los directivos del proyecto deben hacer un estudio de factibilidad para conocer los ingresos y la cantidad, con fines educacionales vamos a utilizar un ingreso de 67 (mil Ether) con un total de 100 (millones de tokens).
Si escogemos esta función para la oferta de un token: f (X) = eax - 1
El eje horizontal (x) representa la cantidad de token en el mercado en millones.
El eje vertical (Y) representa el ingreso en miles de Ether,
El área bajo la curva que describe la función f(X), desde X = a hasta X = b representa el ingreso (I):
I = (Precio) (cantidad) = A = Área bajo la curva
Formulación de nuestro caso:
X = a = 0
X = b = 100
f (X) = eax - 1
A = 67 (mil Ether)
Solución:
Resolviendo por el método de sustitución de variable U = aX
Derivando ambos lados du = a dx
Con las fórmulas de integración de funciones exponenciales
Resulta la ecuación: 67 = 1/a [e100a - (100 a + 1)] aplicando el método de prueba y error:
El valor de a = 0.0095 corresponde un ingreso de:
I = A = 67 (mil Ether)
Ecuación para determinar precios (Y) en función de la cantidad del token (X):
Y = e0.0095 X - 1
Ecuación para determinar el ingreso (I) en función de la cantidad del token (X):
Multiplicar ambos lados por X:
X Y = X (e0.0095 X - 1)
como X Y = I = Ingreso
I = X (e0.0095 X - 1)
El método de prueba y error permite resolver esta ecuación implícita:
Para un ingreso determinado, suponer un valor de X que es la cantidad (en millones de tokens).
Paso 1: Ingreso de 10 mil Ether.
Cuando el ingreso sea de 10,000 Ether, habrá en el mercado 30 millones de tokens.
Paso 2: Ingreso de 20 mil Ether.
Cuando el ingreso sea de 20,000 Ether habrá en el mercado 42 millones de tokens.
Paso 3: Ingreso 30 mil Ether.
Cuando el ingreso sea de 30,000 Ether, habrá en el mercado 50 millones de tokens. Seguimos así hasta alcanzar el ingreso de 67,000 Ether.
Cuando el ingreso sea de 67,000 Ether habrá en el mercado 71 millones de tokens.
Resultados del modelo
1. Resumen de los resultados anteriores:
La emision inicial es de 30 millones de tokens, la segunda de 12 millones, la tercera 8 millones y la ultima emision de 4 millones y se alcanza el total de 71 millones de tokens en el mercado.
2. Aplicando la ecuacion del precio Y = e0.0095 X - 1
Los primeros 30 millones de tokens se venden a 1,300 Ethers y el precio va en aumento hasta alcanzar los 1,963 Ethers.
3.El porcentaje de emision con respecto a los tokens en el mercado, se hace cada vez, menor, lo que convierte al token en un bien escaso y por eso el precio aumenta.